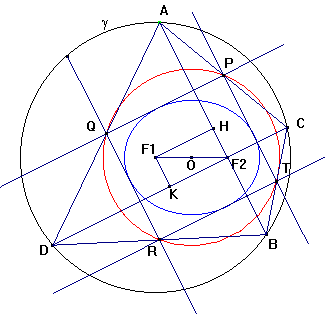
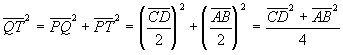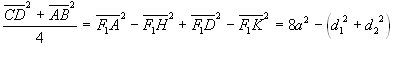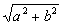DIMOSTRAZIONE Curve ortottiche: caso della ellisse

Sia data l’ellisse di semiassi a e b, fuochi F1 ed F2 (F1F2=2c) e cerchio direttore γ (centro in F1 e raggio 2a). AB e CD sono due corde perpendicolari passanti per F2 . Gli assi dei segmenti F2A, F2B, F2C e F2D sono tangenti all’ellisse (proprietà del cerchio direttore ). I vertici del rettangolo PQRT, circoscritto all’ellisse, cadono nei punti medi dei lati del quadrilatero ABCD e le diagonali del rettangolo si intersecano nel centro O dell’ellisse (per ragioni di simmetria). Si ha: . Condotti da F1 i segmenti di perpendicolare F1H=d1 e F1K=d2 rispettivamente ad AB e CD si ha: . Ma: d1 2+d2 2=F1F2 2=4c2 da cui: QT2=8a2-4c2⇒QO2=2a2-c2=a2+b2=cost. I vertici dei rettangoli circoscritti alla ellisse (punti di intersezione di due tangenti perpendicolari) appartengono sempre alla circonferenza di centro O e raggio  (ortottica).