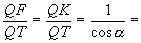DIMOSTRAZIONE Curve isottiche: caso della parabola (1°)

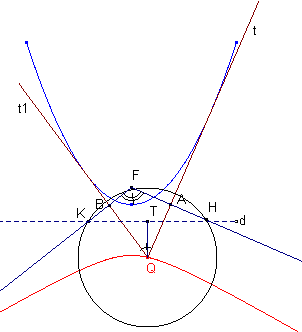
Sia t la tangente alla parabola in un suo punto (asse del segmento FH ove H č il piede della perpendicolare condotta dal punto di tangenza alla direttrice). La tangente t1 che forma con la t un angolo α č l’asse del segmento FK (K sulla direttrice d) tale che KFH=π-α. Il punto Q di intersezione della t con la t1 č il circocentro del triangolo FKH quindi QF=QK=QH; inoltre, essendo BQF+FQA=α si ha KQH=2α. Condotta da Q la perpendicolare QT a KH si ha KQT=α Segue che: cost.>1. Il punto Q descrive una iperbole avente un fuoco in F e una direttrice coincidente con d.