Coniche luogo nel piano: ELLISSOGRAFO DI PROCLO (O "A BARRA"): CONIUGAZIONE ORTOGONALE. ELLISSOGRAFO "A BARRA": CONIUGAZIONE OBLIQUA

I due ellissografi utilizzano il seguente teorema: Se una retta, sulla quale è fissato un segmento, si muove in modo che gli estremi del segmento percorrano due rette fissate nel piano, ogni altro punto della retta stessa percorre una ellisse. A quanto riferisce Proclo nel suo commento al primo libro degli Elementi di Euclide, questa generazione della ellisse era già nota agli antichi Greci: il teorema si ritrova, per il caso di due rette ortogonali, in Guidubaldo Del Monte (fig. 1) (1579), in Stevin (1605) e in Van Schooten (fig. 2) (1657); per il caso di due rette oblique, in Van Schooten (fig. 3) (1657) e in De Witt (1659). In seguito, gli studiosi di cinematica e di geometria del movimento (De La Hire, Bernoulli, Cauchy, Chasles ecc.) hanno analizzato la situazione che si ottiene (ceteris paribus) vincolando rigidamente un piano alla retta mobile (moto relativo di due piani sovrapposti, a guide rettilinee ortogonali od oblique). Si è trovato che: a) Ogni punto del piano vincolato alla retta mobile descrive sull'altro piano una ellisse; b) Ogni punto del piano che contiene le guide rettilinee descrive sull'altro lumache del Pascal; c) La retta mobile inviluppa durante il suo movimento particolari curve quadricuspidate (asteroidi rette od oblique); d) I movimenti generati dalle guide ortogonali e da quelle oblique (apparentemente diversi) sono in realtà identici; e) Il medesimo movimento relativo dei due piani si può ottenere vincolando il primo a una circonferenza che rotola senza strisciare entro un'altra circonferenza (di raggio doppio) fissata al secondo piano.
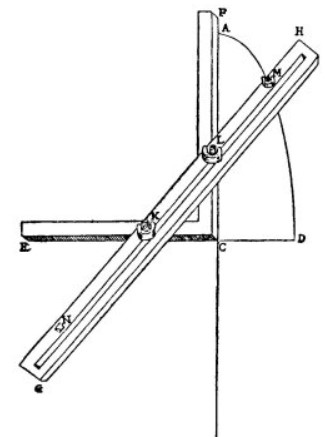
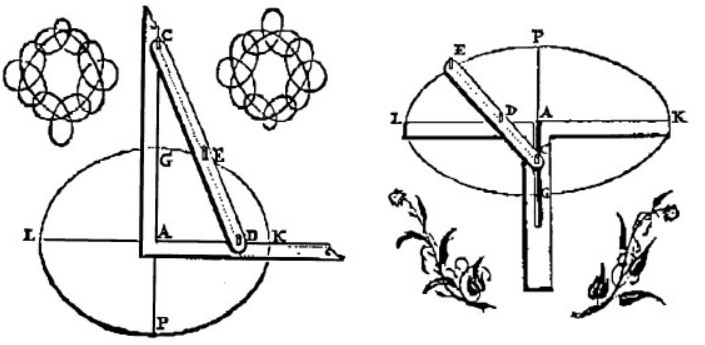
Fig. 1 da G. Del Monte, Planisphaeriorum Fig. 2 da F. van Schooten, Exercitationum Mathematicarum libri quinque, Leiden, 1657.
universalium theorica, 1579.

Fig. 3 da F. van Schooten, Exercitationum Mathematicarum libri quinque, Leiden, 1657.

