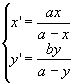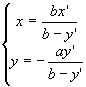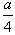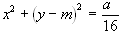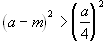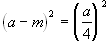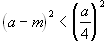DIMOSTRAZIONE Teorema di Stevin: proiezione di una circonferenza in una parabola

Una prova (analitica) richiede le equazioni della omologia (usiamo per semplicità quelle canoniche), cioè (De La Hire): (*)  (per trasformare i punti); (**)  (per trasformare le equazioni). Si consideri la circonferenza di raggio  e centro (variabile) S(0,m) con equazione  e si applichino ad essa le (**). Dopo qualche calcolo si ricava che, se  la curva trasformata è una ellisse; se  la curva trasformata è una parabola; se infine  è una iperbole. Nei tre casi la retta limite y=a e la circonferenza sono rispettivamente non secanti, tangenti, secanti.