Genesi tridimensionale di trasformazioni: inversione circolare
Il modello illustra la genesi spaziale tridimensionale della inversione circolare. Proiettando da due poli opposti O1 e O2 di una sfera S (di centro O e raggio r) uno stesso punto A della sfera su un piano π perpendicolare a O1O2 (ad esempio il piano diametrale, come nel modello) si ottengono i punti P e Q (proiezioni stereografiche di A su π, rispettivamente da O2 e O1 ). P e Q si corrispondono nella inversione circolare rispetto alla circonferenza γ intersezione di S con π. Il modello mostra inoltre che le proiezioni (da O1 e O2 ) su π dei punti di una circonferenza C0 di S passante per O1 appartengono ad una retta r (proiezione di C0 da O1 ) e ad una circonferenza C passante per O (proiezione di C0 da O2 ). C ed r si corrispondono nella inversione circolare rispetto a γ.

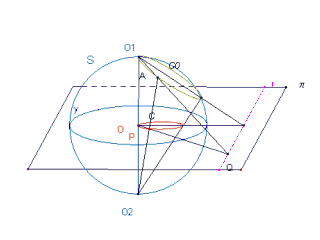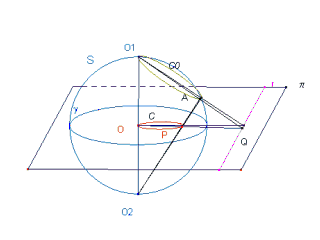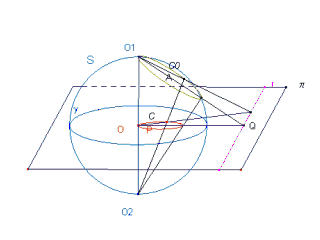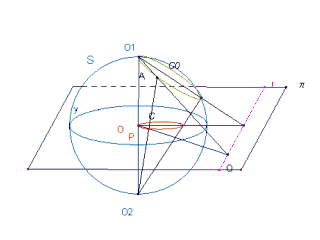
INVERSIONE CIRCOLARE - Dim. in cm 87 X 68 X 38
(vedi rif. Definizioni e proprietą: Inversione circolare, polaritą circolare (nel piano euclideo))

