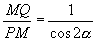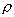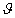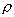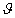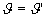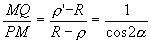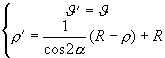DIMOSTRAZIONE Anamorfosi per riflessione. Cono
Su π si corrispondono il cerchio γ di base del cono (luogo dei punti P) e la corona circolare di centro O, raggio interno Ri=R e raggio esterno 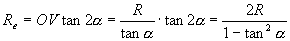
Poiché δ n, δ’ (δ: raggio luminoso uscente dalla sorgente S, incidente sullo specchio in A; δ': raggio riflesso; n: normale allo specchio in A) appartengono al piano passante per A e per l’asse del cono , se ne deduce che, in ogni posizione, i punti P e Q sono allineati con O. Inoltre, siccome
l’angolo di incidenza è uguale all’angolo di riflessione si ha: 
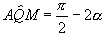
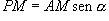
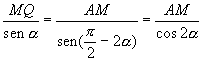
Quindi