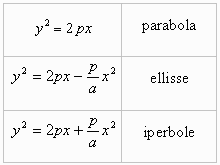Ti trovi qui:
Home » Laboratorio Visite Mostre » La collezione di Macchine Matematiche » 4. Curvigrafi
Definizioni e proprietà: CONICHE
Ricordiamo alcune proprietà che occorre avere presenti per comprendere il funzionamento dei principali conicografi:
-
I "sintomi"
usati dai geometri greci per caratterizzare le coniche sono da noi espressi mediante le equazioni:
Queste equazioni valgono sia in coniugazione ortogonale (assi cartesiani ortonormali, asse y tangente alla curva in un vertice) sia in coniugazione obliqua (assi cartesiani obliqui, asse y tangente alla curva in un estremo del diametro sovrapposto all'asse x).
Significato dei simboli: p è il lato retto relativo al diametro assunto come asse delle ascisse;
2a è la lunghezza di tale diametro (in coniugazione ortogonale, è l'asse maggiore dell'ellisse, l'asse reale dell'iperbole).
Vedi modelli: Conicografi del Cavalieri: parabola; ellisse; iperbole; Macchina di Oddi-Paciotti, Parabolografo di De l'Hospital, Iperbolografo di De l'Hospital. -
L'ellisse è il luogo dei punti di un piano per i quali è costante la somma delle distanze da due punti fissi del piano stesso (fuochi).
L'iperbole è il luogo dei punti di un piano per i quali è costante la differenza delle distanze da due punti fissi del piano stesso (fuochi).
La parabola è il luogo dei punti di un piano equidistanti da un punto e da una retta del piano stesso.
Vedi modelli: Parabolografo a filo teso; Ellissografo a filo teso; Iperbolografo a filo teso (1) e (2); Ellissografo ad antiparallelogramma; Iperbolografo ad antiparallelogramma. - Il luogo dei punti di un piano per i quali è costante il rapporto "e" delle distanze da un punto (fuoco) e da una retta (direttrice) del piano stesso è una ellisse, una parabola o una iperbole, secondo che il detto rapporto "e" (eccentricità) è minore, uguale o maggiore di 1.
-
Chiamiamo circoli direttori dell'ellisse e dell'iperbole i circoli aventi il raggio uguale all'asse principale e per centro uno dei fuochi.
Il luogo dei punti simmetrici di un fuoco di una ellisse o di una iperbole rispetto alle tangenti della medesima è il circolo direttore che ha per centro l'altro fuoco. L'ellisse, o l'iperbole, è il luogo dei punti equidistanti da un suo fuoco e dal corrispondente circolo direttore.
Vedi modelli: Conicografi che utilizzano il cerchio direttore: parabola; ellisse; iperbole. -
La podaria di un fuoco di una conica centrale rispetto alla conica stessa è il circolo che ha per diametro l'asse principale. La podaria del fuoco di una parabola rispetto alla parabola stessa è la tangente nel vertice.
Vedi modelli: Generazione di inviluppi: metodo della podaria: parabola; ellisse; iperbole. -
Se N è il punto di incontro della normale in un punto P ad una parabola con l'asse della medesima, la proiezione del segmento PN sull'asse della parabola (sottonormale relativa all'asse) è uguale alla distanza del fuoco dalla direttrice. Se K è la proiezione sull'asse della parabola di un punto P della medesima, T il punto di incontro dell'asse con la tangente in P, il vertice V della parabola divide per metà il segmento KT (sottotangente relativa all'asse).
Vedi modelli: Parabolografo (proprietà della sottonormale e sottotangente) -
Il parallelogrammo che ha per lati i due asintoti di una iperbole e le parallele ad essi condotte da un punto qualunque della curva stessa ha area costante.
È costante l'area del triangolo formato dai due asintoti di una iperbole e da una tangente qualsiasi della medesima. L'area del parallelogrammo che ha per diagonali due diametri coniugati di una ellisse è costante.
L'area del parallelogrammo che ha per mediane due diametri coniugati di una ellisse è costante. -
Teorema di PASCAL (esagono "mistico") Si trovava nel "Trattato sulle coniche", manoscritto perduto di Pascal, che noi conosciamo solo attraverso alcuni estratti e una breve analisi contenute in una lettera di Leibniz a E. Périer.
Nel linguaggio contemporaneo, eccone l'enunciato:
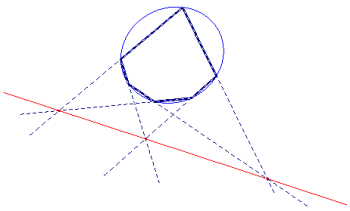
"Se un esagono semplice è iscritto in una conica, le intersezioni delle tre coppie di lati opposti stanno sopra una stessa retta (retta di Pascal); e viceversa, se in un esagono semplice si verifica l'ultima proprietà, i vertici di esso appartengono a una stessa conica, (che può anche degenerare in due rette)".
Caso particolare: "in un esagono semplice iscritto in una circonferenza, le intersezioni delle tre coppie di lati opposti sono allineate".
Conviene dimostrare prima questo caso, poi, per proiezione, estendere alle coniche la validità dell'enunciato.
Vedi modelli: Generazione organica delle coniche secondo McLaurin: ellisse.