DIMOSTRAZIONE Ellissografo a barra: guide ortogonali

(Dimostrazione TEOR.1)
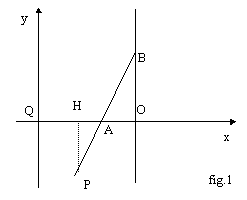
(Fig. 1) Per i punti della retta AB (interni od esterni all’asta in movimento) ci si può richiamare ai metodi classici (teoria delle proporzioni). Sia per esempio P un punto esterno al segmento AB; sia inoltre QO= PA+AB, H la proiezione ortogonale di P su QO. Vale ovviamente la proporzione HA:PA=AO:AB. Questa, ponendo per comodità QH=x, HP=y, PA=a, AB=b si può scrivere: . Con semplici calcoli (prodotto dei medi = prodotto degli estremi; elevamento al quadrato; semplificazioni) si ricava la proprietà caratteristica che definisce una ellisse. (Fig. 2) Per un punto generico P di σ conviene ricorrere alla trigonometria. Si noti che P può in ogni caso essere raggiunto mediante un percorso costituito da due segmenti consecutivi BH (AH) e HP ortogonali fra loro (BH oppure AH sono sul prolungamento di AB). Nell’esempio della figura si ponga: AB=b, BH=a, HP=c; si assumano come assi cartesiani le due scanalature; sia α l’angolo tra AB e l’asse delle ascisse. Le coordinate x, y di P si esprimono come segue: x = a cos α+ c sen α, y = (a+b) sen α- c cos α. Eliminando il parametro si ottiene un polinomio del tipo a11x2 + 2a12xy + a22y2 + a33 = 0, il cui discriminante è - (a2 + c2 + ab)2 . Si tratta perciò dell’equazione di una ellisse.

 

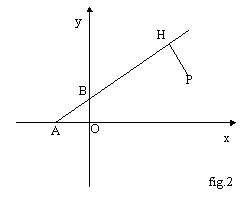
(Dimostrazione TEOR.2)
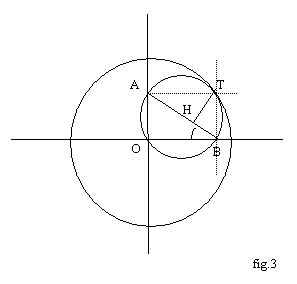
(Fig.3) Supponiamo che il moto dei due piani sia realizzato facendo rotolare senza strisciare (l’una sull’altra) una circonferenza di diametro AB (passante per O, fissata a α) e una circonferenza di centro O e raggio AB (fissata a π). Sia T il punto di contatto fra le due circonferenze; T è anche il centro istantaneo di rotazione dell’asta AB=b; quindi, condotta da T la perpendicolare ad AB, il piede H di tale perpendicolare è punto di contatto tra AB e la curva inviluppata. (Siccome T è vertice del rettangolo di lati OA, OB si ottiene anche una semplice costruzione per punti di tale curva). Equazione della retta AB: 2xsen α + 2ycos α = b sen 2α (essendo α l’angolo tra AB e la scanalatura OB assunta come asse delle ascisse): per determinarla, partire dalla equazione segmentaria della retta AB e applicare il teorema dei seni al triangolo PAB. Equazione della retta per T perpendicolare ad AB: (y - b sen α)sen α + (x - b cos α)cos α = 0. Si ricavano per H le coordinate, x = b cos3 α, y = b sen3 α (equazioni parametriche dell’asteroide retto). Si noti che rette diverse da AB inviluppano asteroidi obliqui.

 

(Dimostrazione TEOR.3)
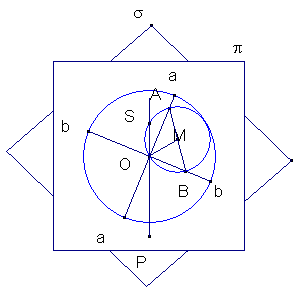
Sul piano mobile π, si consideri la intersezione O tra le scanalature aa, bb che scorrono entro i perni A e B fissati su σ. Si tracci in π una retta OP (P punto generico di π) la quale intersechi in S la circonferenza di diametro AB (centro M). L’angolo SOA è costante: quindi , mentre O percorre la circonferenza avente AB come diametro, su questa S si mantiene a distanza fissa da AB. Si può allora costruire il seguente biellismo: una sbarra MO è imperniata in M e incernierata in O a un’asta sovrapposta ad OP e vincolata a scorrere entro un cursore collocato in S. Questo biellismo coincide con quello che traccia le "lumache" del Pascal.