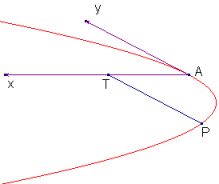
DIMOSTRAZIONE Sezioni coniche (Apollonio): parabola
Se EF è l'intersezione del piano
secante s con il piano di base b, si
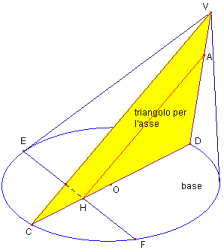
considera un triangolo per l'asse
VDC tale che DC sia perpendicolare a EF.
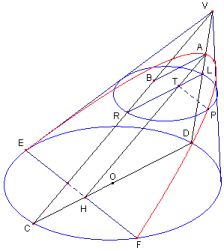
Sia AH l'intersezione di VDC con s. Nel piano b' condotto per P e parallelo
al piano di base del cono, si ha
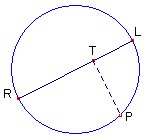
per il teorema di Euclide:
(1) PT2 = RT·TL;
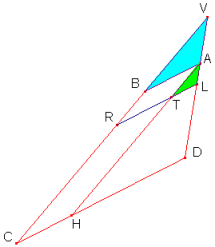
nel piano t si ha:
(2) BA = RT;
(3) VAB simile a VDC da cui: BA : VA = CD : VD,
cioè RT : VA = CD : VD.
(4) ALT simile a VDC da cui: TL : AT = CD : VC.
Moltiplicando la (3) e la (4):
(5) (RT·TL) : (VA·AT) = CD2 : (VD·VC), cioè
PT2 : (VA·AT) = CD2 : (VD·VC).
Si costruisca un segmento k tale che:
(6) CD2 : (VD·VC) = k : VA. Si ha:
(7) PT2 : (VA·AT) = k : VA da cui si ricava
(k·VA·AT) = (PT2·VA)
cioè
(8) PT2 = k·AT.
Posto AT=x, PT=y la 8) si può scrivere
y2 = kx
(in un riferimento cartesiano con origine in A e assi obliqui).