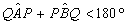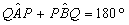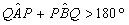DIMOSTRAZIONE Generazione organica delle coniche secondo Newton. Ellisse
Si assuma un riferimento cartesiano in cui s è l'asse delle ascisse , A è sull'asse delle ordinate. Scritte le equazioni dei tracciatori in funzione di t, ascissa del punto direttore Q, e delle tangenti trigonometriche degli angoli QAP e PBQ, si ottengono facilmente nei tre casi
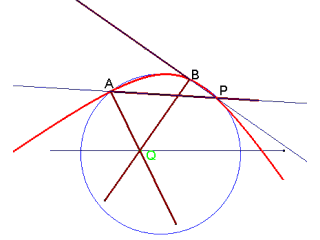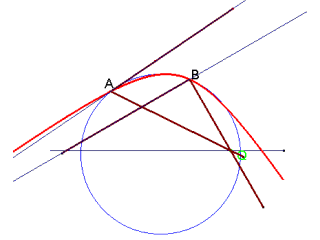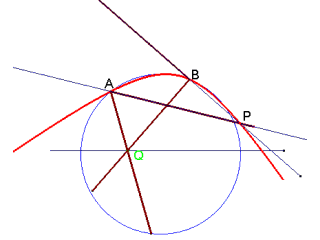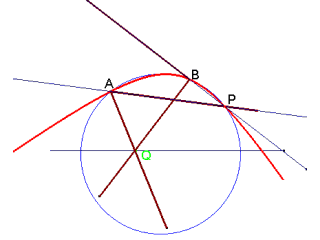
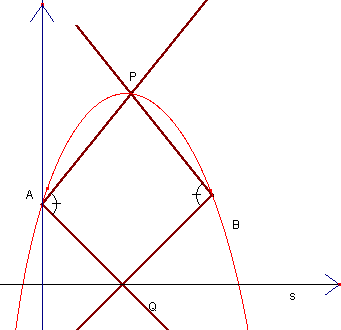
(In figura è rappresentato il caso 3) le equazioni parametriche della curva tracciata da P (ma i calcoli sono fastidiosi). E' più semplice (per chi conosce la geometria proiettiva) ricavare dalle condizioni imposte la relazione che lega i coefficienti angolari dei tracciatori e osservare che è bilineare (i fasci cui appartengono AP e BP sono proiettivi). Cercando le direzioni unite nella proiettività si deduce la natura delle curve.
Teorema di Mac Laurin:
Si costruisca sul segmento AB un segmento circolare capace dell'angolo 2π-(PAQ+QBP) e si tracci il cerchio C cui tale segmento appartiene. Se C interseca la retta direttrice s, P descrive una iperbole. Se C è tangente ad s, P descrive una parabola, altrimenti C descrive una ellisse.
Se le ipotesi del teorema sono verificate, si deduce che quando Q si trova nei punti di inetersezione della circonferenza C con la retta direttrice, le rette che sostengono i lati tracciatori sono parallele. Quando tali punti di intersezione sono due, la conica descritta da P ha quindi due punti impropri distinti (iperbole), quando sono due coincidenti ha un solo punto improprio (parabola) altrimenti è una ellisse.