DIMOSTRAZIONE Parabole che rotolano l'una sull'altra senza strisciare
Il punto F', fuoco della parabola P', simmetrica della P rispetto alla tangente t in un suo punto T qualsiasi, appartiene sempre alla direttrice d della P: infatti F' è simmetrico di F rispetto a t , quindi TF=TF' e poichè t è bisettrice dell'angolo FTF', TF' è in ogni posizione perpendicolare a d. L'asse a di P è parallelo ad F'T, l'asse a' di P' è parallelo ad FT, la perpendicolare ad a condotta per F ha distanza costante (FH) da F', così la perpendicolare ad a' condotta per F' ha distanza (FK=FH) costante da F. La retta F'K è in ogni posizione tangente alla circonferenza di centro F e raggio FH. Il punto Q di intersezione fra t e il segmento che congiunge i vertici delle due parabole descrive una cissoide, podaria di P rispetto a V. V' è in ogni posizione il corrispondente di Q in una omotetia di centro V e rapporto 2, quindi descrive anch'esso una cissoide.
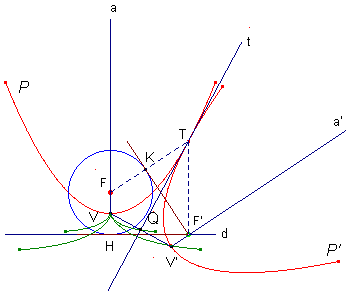
La podaria di una parabola rispetto al suo vertice è una cissoide.
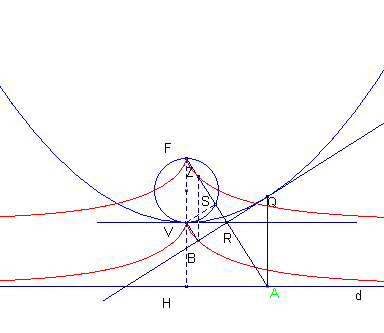
Siano F e d rispettivamente fuoco e direttrice di una parabola P . Sia Q il punto di intersezione dell'asse del segmento FA con la perpendicolare a d condotta per A : quando A percorre d, Q descrive la parabola P e la QR (R punto medio di FA) è tangente alla parabola in Q.
Siano:
- B il piede della perpendicolare condotta dal vertice V della parabola a tale tangente.
- S il punto di intersezione della FA con la circonferenza di diametro FV.
- Z il punto di intersezione della parallela ad FH (tracciata per B) con FA.
I triangoli FSV e ZRB son uguali, quindi ZR=FS. Z descrive allora una cissoide C. Essendo BZ=VF, B è il corrispondente di Z nella traslazione individuata dal vettore FV quindi descrive la cissoide traslata della C.