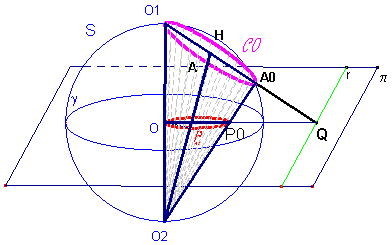
DIMOSTRAZIONE Genesi tridimensionale di trasformazioni: inversione circolare
I punti P e Q sono corrispondenti nella inversione circolare rispetto a γ. Infatti, dalla similitudine dei triangoli rettangoli O1OQ e O2OP (O1AO2=90°) si ha: O1O/OQ=OP/O2O da cui: OP*OQ=O1O*O2O=r2 (r, raggio di S, è anche raggio di γ). Inoltre, poiché O1 , O2 e A appartengono allo stesso piano, i punti O, P e Q sono allineati.
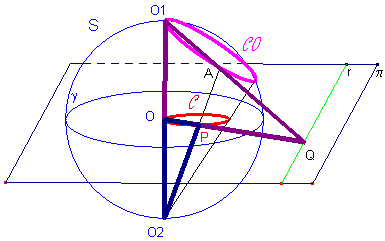
La circonferenza C e la retta r sono corrispondenti nella inversione circolare rispetto a γ. La circonferenza C0 appartiene ad un piano (α) passante per O1 che interseca π secondo una retta r. Le proiezioni dei punti di C0 da O1 appartengono ad r. I raggi che da O2 proiettano i punti di C0 generano un cono circolare; sia H il punto di intersezione dell’asse del cono con il piano α di C0 . Prolungato O1H fino ad incontrare C0 (e anche S) nel punto A0 , il triangolo O1O2A0 è il triangolo per l’asse del cono relativamente alla sezione con α. Indicata con P0 la proiezione stereografica di A0 su π (dal polo O2 ) il triangolo OO2P0 è il triangolo per l’asse del cono relativamente alla sezione con π. Poiché i triangoli O1O2A0 e OO2P0 sono simili, le sezioni del cono con i piani α e π sono della stessa natura (teorema di Apollonio: libro 1°, teorema n.5) quindi C è una circonferenza (passante per O). La circonferenza C e la retta r, luoghi delle proiezioni stereografiche dei punti di C0 su π (rispettivamente da O2 e da O1 ) sono corrispondenti nella inversione circolare rispetto a γ.