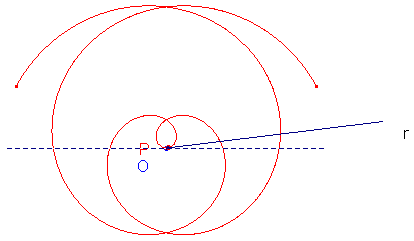
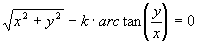DIMOSTRAZIONE Generazione di curve trascendenti. Spirali di Archimede (metodo di Clairaut)
Un attimo di riflessione basta a chiarire che la generazione precedente equivale a quella classica: "Una retta r si muova in un piano ruotando attorno a un punto fisso O con velocità angolare costante; un punto P percorra la retta r con velocità uniforme partendo da O. Il punto P descriverà allora una curva che passa per O, fa infinite circonvoluzioni intorno ad O e si chiama Spirale di Archimede". Nel modello proposto la sincronizzazione dei due movimenti è "automatica": non è dunque necessario che β rotoli con velocità angolare costante. Altra differenza: nella definizione classica il secondo ramo della curva si ottiene invertendo la rotazione di r; nel modello proposto si passa da un "ramo" all'altro quando (seguitando β a rotolare nel medesimo verso) P attraversa il centro di β. I due rami della curva si tagliano determinando infiniti punti doppi allineati su un asse di simmetria della curva stessa. Assumiamo come polo il punto fisso O; come asse polare la posizione iniziale della retta r: si ha subito la equazione polare ρ=k∞, (k>0 costante); alla quale corrisponde l'equazione cartesiana: