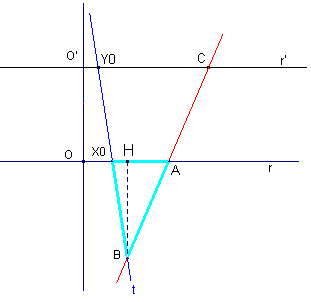
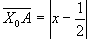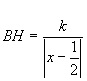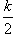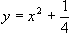DIMOSTRAZIONE Generazione di inviluppi: metodo della corrispondenza. Iperbole

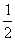
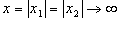
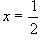
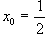
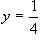
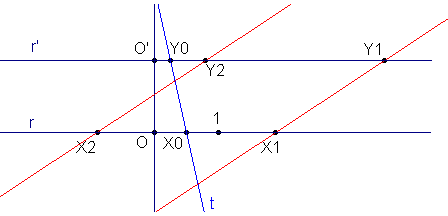
Le rette dell’inviluppo sono a due a due parallele: infatti scelti due punti X1 (ascissa X1 ) e X2 (ascissa X2 ) sulla retta r simmetrici rispetto al punto X0 di ascissa , le rette congiungenti X1 e X2 con i loro corrispondenti Y1 e Y2 sulla retta r’ sono parallele: infatti la condizione di parallelismo X1 2-X2 2=X1 -X2 è soddisfatta se X2 =1-X1 . Per  le due tangenti parallele tendono a sovrapporsi alla retta r. Per  le tangenti parallele coincidono sulla retta t dell’inviluppo congiungente il punto X0 () sulla retta r con il punto  (sulla r’). Se la curva inviluppata è una iperbole le rette r e t sono i suoi asintoti.

Considerata ora una generica retta dell’inviluppo , indicate con A e B rispettivamente le intersezioni con le rette r e t si può verificare che il triangolo X0AB ha area costante: infatti  e dalla similitudine dei triangoli BAX0 e BCY0 si ha , ove k è la distanza fra le rette r ed r’, quindi l’area del triangolo X0AB è  (proprietà caratteristica dell'iperbole). La curva γ inviluppata è dunque un’ iperbole con centro nel punto X0 e avente per asintoti le rette r e t. Applicando alla retta r’ una qualsiasi traslazione. la curva γ' inviluppata è ancora una iperbole. Infatti γ e γ' si corrispondono in una omologia affine di asse r che trasforma r’ nella r" ottenuta con la traslazione. Se la retta r’ viene traslata in modo tale che la perpendicolare ad r ed r’ condotta per O’ intersechi in X0 la retta r , l’iperbole inviluppata è equilatera. Ciò equivale a rappresentare sulle rette r ed r’ la funzione .