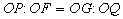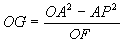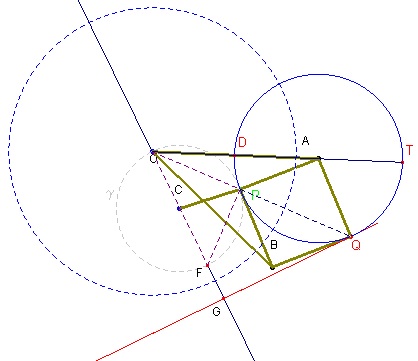
DIMOSTRAZIONE Proprietà della inversione circolare: guida rettilinea

Tracciata la circonferenza di centro A e raggio AQ, per il teorema delle secanti si ha:
OP·OQ = OD·OT =
= (OA - AD)·(OA + AD) =
= OA2 - AD2.
Sia C il centro della circonferenza passante per O e descritta da P. Sia F l’estremo del diametro per O e sia G il suo corrispondente nella inversione circolare. Si ha:  e . I triangoli OPF e OGQ sono quindi simili e OGQ è un angolo retto. Q descrive allora la retta perpendicolare ad OF e passante per G ove .