Coniche luogo nel piano: PARABOLOGRAFO A FILO TESO

Questo strumento a filo, che De L'Hospital impiega nel suo trattato sulle sezioni coniche (ed. 1720) per definire la parabola, è descritto da Kepler ("Ad Vitellionem Paralipomena", ed. 1604) insieme a quelli (più facili da ideare perchè implicitamente contenuti nelle proposizioni 51 e 52 del libro III° di Apollonio) che tracciano ellissi ed iperboli: in modo particolarmente interessante perchè fa ricorso al concetto di infinito attuale e al codice dell'analogia. "A lungo mi dolsi" - scrive Kepler - di non saper descrivere col filo anche una parabola: finalmente l'analogia mi mostrò una soluzione". Se infatti si immagina una parabola di fuoco F come una ellisse avente uno dei fuochi in F e l'altro a distanza "infinita" da F (sicchè la retta che lo congiunge a un punto P della curva diventa parallela all'asse di questa), sia la somma delle distanze dei due fuochi da P, sia la loro differenza, è una semiretta: che può essere considerata di lunghezza costante. Quindi è possibile immaginare la parabola anche come iperbole. Poichè la parabola è il luogo dei punti equidistanti da una retta (direttrice) e da un punto ad essa esterno (fuoco), nello strumento costruito per "analogia" con un ellissografo (fig. 1-2) o iperbolografo (fig. 3-4-5) la lunghezza totale del filo teso risulta pari alla distanza fra la direttrice e una retta a questa parallela (base del segmento parabolico tracciato).
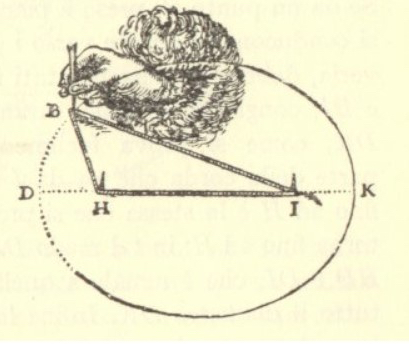
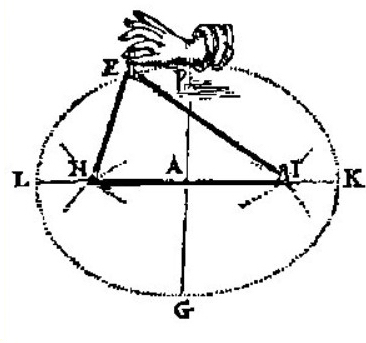
Fig. 1 da R. Descartes, La dioptrique, 1636. Fig. 2 da F. van Schooten, Exercitationum Mathematicarum libri quinque, Leiden, 1657.
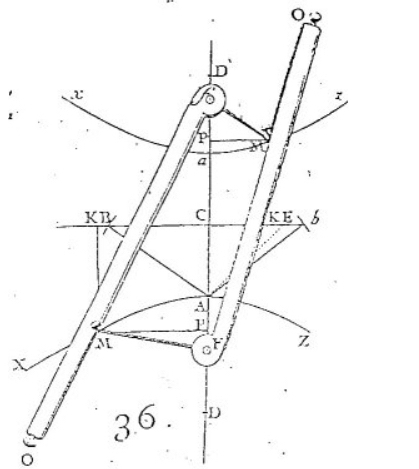
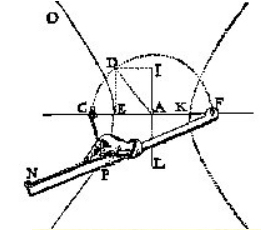
Fig. 3 da G.F.A. De L'Hospital Theorie analytique Fig. 4 da F. van Schooten, Exercitationum Mathematicarum libri quinque, Leiden, 1657.
des sections coniques, Paris 1720.

Fig. 5 da R. Descartes, La dioptrique, 1636.

