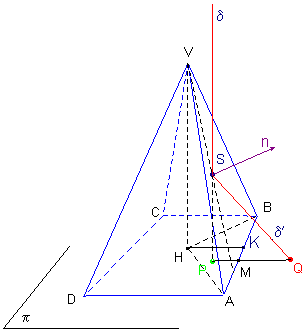
DIMOSTRAZIONE Anamorfosi per riflessione. Piramide

Le equazioni della corrispondenza che porta una figura F in una figura F' disegnata sulla regione di piano esterna alla piramide si ricavano come segue:
1) Calcolo relativo alla faccia VAB
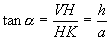
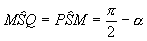
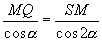
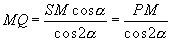
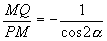
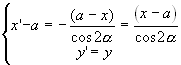
I raggi δ e δ’ appartengono al piano normale alla faccia VAB in S e parallelo al piano del triangolo VHK quindi i punti P e Q giacciono sulla stessa perpendicolare in M ad AB. Indicato con α l’angolo PMS=HKV si ha: . Inoltre , per le proprietà della riflessione si ha:  da cui: . Nel triangolo PSM è PM=SMcosα . Nel triangolo SMQ è  perciò . Quindi . Riferito il piano π ad un sistema di assi cartesiani con origine in H e asse x coincidente con HK e indicate con (x,y) le coordinate di P e con (x’,y’) quelle di Q si hanno le equazioni: 

2) Si procede analogamente per le altre facce.
La costruzione può essere eseguita con riga e compasso: si tratta infatti di una omologia affine (stiramento).