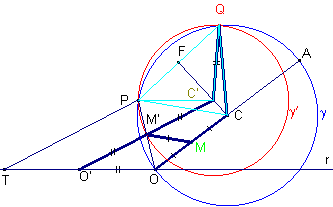
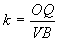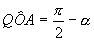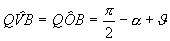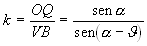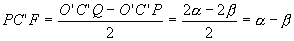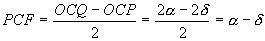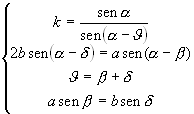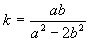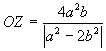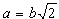DIMOSTRAZIONE Guida rettilinea di Hart (2°)
Si consideri un caso più generale; sia OO’=O’M’=a, OM=MM’=b , O’C’=2a, OC=2b. Il punto Q è una delle intersezioni della circonferenza γ (centro C e raggio 2b) con la circonferenza γ' (centro C’ e raggio a). L’ulteriore intersezione P delle due circonferenze è il punto simmetrico di O rispetto ad M’. Infatti : indicato con S il simmetrico di O rispetto ad M’, dalla similitudine dei triangoli OM’M e OSC si ha SC=2b e dalla congruenza dei triangoli O’OM’ e M’SC’ si ha SC’=a e quindi S coincide con P. P descrive una circonferenza. Infatti: condotta da P la parallela ad O’C’ e indicata con T l’intersezione con la retta r si ha: TP=TO=2a. Anche Q descrive una circonferenza. Si prolunghi OC e sia A l’intersezione con γ, si congiunga Q con O e con A e si prolunghi QA fino ad incontrare in Z la retta r. La circonferenza γ interseca la retta r nei punti O e B e la retta QC in V. I triangoli OQZ e QVB sono simili (infatti entrambi sono rettangoli e QÔZ=QVB). Poichè QVB ha ipotenusa costante, anche OZ è costante e Q descrive la circonferenza di diametro OZ. Calcoliamo il valore del rapporto di similitudine costante. Sia